Python

ARIMA

ARIMA(자기회귀 통합 이동 평균)

자기회귀(AR) 구성요소(p)

  • 자기회귀 구성 요소는 관찰과 일부 지연된 관찰(이전 시간 단계)간의 관계 캡처
  • “p”라는 용어는 자기회귀 구성요소의 순서를 나타내며, 고려되는 지연된 관측치 수

통합(I) 구성요소(d)

  • 통합 구성 요소에는 시계열 데이터를 차별화하여 고정시키는 작업이 포함,

    정상성은 평균, 분산 등 시계열의 통계적 속성이 시간이 지나도 변하지 않는 것을 의미
  • “d”라는 용어는 정상성을 달성하는 데 필요한 차분의 차수

이동평균(MA) 구성요소(q)

  • 이동 평균 구성 요소는 시차 관측에 적용된 이동 평균 모델의 관측과 잔차 오차 간의 관계를 나타냄
  • “q”라는 용어는 이동 평균 성분의 차수를 나타내며, 시차 잔차가 얼마나 고려되는지 나타냄
  • p : 자기회귀 구성요소의 순서
  • d : 차분의 순서
  • q : 이동평균 구성요소의 순서
1
pip install statsmodels
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA

# 시계열 데이터 생성
np.random.seed(42)
time = np.arange(100)
data = 2 * np.sin(0.2 * time) + np.random.normal(0, 1, size=100)

df = pd.DataFrame({'Time': time, 'Data': data})

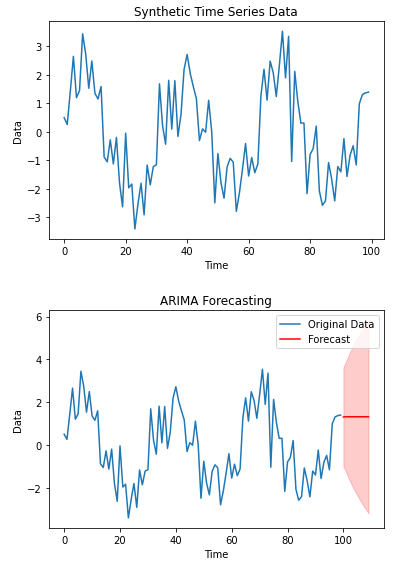
plt.plot(df['Time'], df['Data'])
plt.xlabel('Time')
plt.ylabel('Data')
plt.title('Synthetic Time Series Data')
plt.show()

# ARIMA 모델 fit
order = (1, 1, 1)  # ARIMA(p, d, q) order
model = ARIMA(df['Data'], order=order)
results = model.fit()

# 예측
forecast_steps = 10
forecast = results.get_forecast(steps=forecast_steps)

# 시각화
plt.plot(df['Time'], df['Data'], label='Original Data')
plt.plot(np.arange(100, 100 + forecast_steps), forecast.predicted_mean, label='Forecast', color='red')
plt.fill_between(np.arange(100, 100 + forecast_steps), forecast.conf_int()['lower Data'], forecast.conf_int()['upper Data'], color='red', alpha=0.2)
plt.xlabel('Time')
plt.ylabel('Data')
plt.title('ARIMA Forecasting')
plt.legend()
plt.show()

ARIMA는 계절성, 추세, 노이즈 등 요인에 따라 성능에 영향을 받을 수 있음

Share